Stationarity of time-series stochastic process¶

Main resources used:

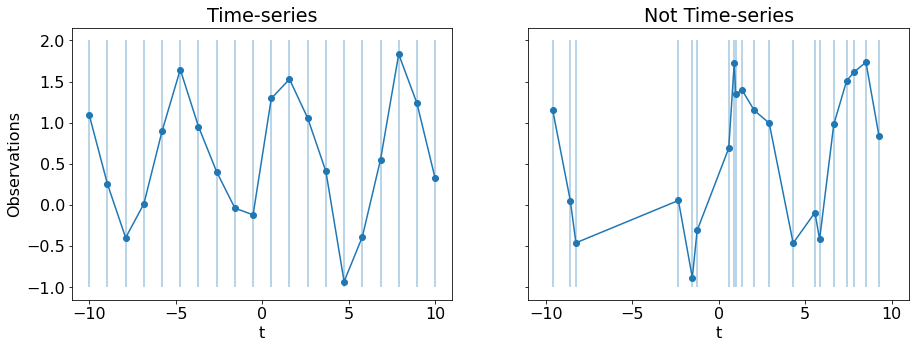
What is a time-series?¶

Observations made at equally spaced time-stamps create a time-series

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rc
from GPy.kern import RBF, Matern32, Matern52, Exponential, ExpQuad

N = 20
l,h=-10,10
np.random.seed(0)
xs = np.linspace(l,h,N)
ys = np.sin(xs) + np.random.rand(N)
np.random.seed(0)
xns = np.sort(np.random.uniform(l,h,N))
yns = np.sin(xns) + np.random.rand(N)

rc('font', size=16)
# rc('text', usetex=True)
fig, ax = plt.subplots(1,2,sharey=True,sharex=True, figsize=(15,5))
ax[0].plot(xs, ys,'o-')
for i in range(N):
    ax[0].vlines(xs[i], -1, 2, alpha=0.4)
    ax[1].vlines(xns[i],-1, 2, alpha=0.4)
ax[1].plot(xns, yns, 'o-');
ax[0].set_xlabel('t');ax[1].set_xlabel('t');
ax[0].set_ylabel('Observations');

ax[0].set_title('Time-series')
ax[1].set_title('Not Time-series');

../_images/2021-03-17-Stationary-Time_Series_4_0.png

What is a stochastic process?¶

A joint probability distribution for a collection of random variables

Connection between time-series and stochastic process¶

A time-series can be treated as a realization (sample) of stochastic process.

Stochastic process	Time-series
Variable	Time-stamp
Sample	Observations

Example \(\to\) A Time-series with 8 time-stamps is a sample taken from joint probability distribution of a stochastic process with 8 variables.

Stationary time-series process¶

First moment (\(\mathbb{E}\)) and second moment (\(V\)) should be constant over time

For all \(t\),

\(\mathbb{E}(y_t) = \mu \) Constant
\(V(y_t) = \sigma^2 \) Constant
\(Cov(y_t, y_{t+h}) = \gamma \) Constant

Why stationarity is important?¶

Autoregressive models for modeling and prediction works best with stationary time-series

How to check for stationarity?¶

Visually
Global v/s local test
Statistical test (Augmented Dickey-Fuller test or Unit root test)

import pandas as pd
from statsmodels.tsa.stattools import adfuller

fig, ax = plt.subplots(1,3,figsize=(15,5))
x = np.linspace(1,10,1000)
y1 = pd.read_csv('../data/international-airline-passengers.csv').values[:,1]
y2 = np.sin(x*5)+x-5
y3 = np.sin(x*5)
ax[0].plot(y1,'o-');
ax[1].plot(x,y2,'o-');
ax[2].plot(x,y3,'o-');
for each in ax[::-1]:
    each.set_xlabel('t')

ax[0].set_title(f'ADF Test p value= {np.round(adfuller(y1[:-1])[1],2)}')
ax[1].set_title(f'ADF Test p value= {np.round(adfuller(y2[:-1])[1],2)}')
ax[2].set_title(f'ADF Test p value= {np.round(adfuller(y3[:-1])[1],2)}')
each.set_ylabel('Y');

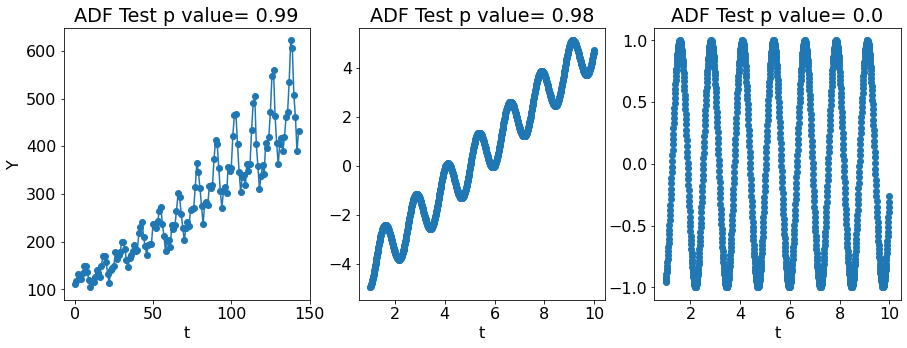
../_images/2021-03-17-Stationary-Time_Series_11_0.png

p-value close to \(1\) means non-stationarity in adfuller test and vice versa.

Linear time-series model¶

\[ X_t = \sum\limits_{i=1}^{p}\phi_iX_{t-i} + \epsilon_t \]

Characteristic equation and unit root¶

AutoRegressive(1) model

(40)¶\[\begin{align} X_t - \phi_1X_{t-1} &= a_t \\ (1-\phi_1B)X_t &= a_t \\ \text{Char. eq.}\\ 1 - \phi_1Z &= 0 \end{align}\]

AutoRegressive(2) model

(41)¶\[\begin{align} X_t - \phi_1X_{t-1} - \phi_2X_{t-2}&= a_t \\ X_t- \phi_1 BX_t -\phi_2 B^2 X_t &= a_t \\ X_t\left[ 1 - \phi_1 B - \phi_2 B^2 \right] &= a_t \\ \text{Char. eq.}\\ 1 - \phi_1 Z - \phi_2 Z^2 &= 0 \end{align}\]

Stationarity¶

if all roots are outside unit circle, we call the process as stationary

How to convert non-stationary Time-series to stationary?¶

Remove known trends
Apply log transform
Take difference series

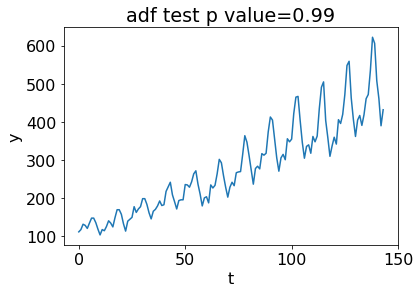
Below is an example of difference series.

plt.plot(y1);
plt.title(f'adf test p value={np.round(adfuller(y1[:-1])[1], 2)}')
plt.xlabel('t');plt.ylabel('y');
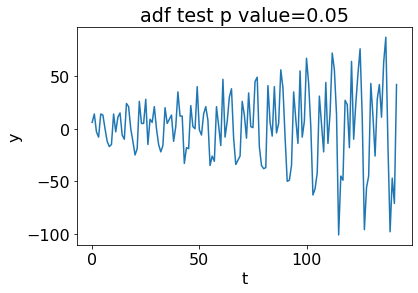
plt.figure();
y11 = y1[:-1]
y11 = y11[1:] - y11[:-1]
plt.plot(y11);
plt.title(f'adf test p value={np.round(adfuller(y11)[1], 2)}');
plt.xlabel('t');plt.ylabel('y');

../_images/2021-03-17-Stationary-Time_Series_19_0.png

../_images/2021-03-17-Stationary-Time_Series_19_1.png

Explain-ML

Stationarity of time-series stochastic process

Contents